%MATLAB ASSIGNMENT 1 : INTEGRALS %-------------PART 1: Riemann sums with fixed lengths--------------- disp('-----------------Part 1-------------------------'); f = @(x) x.^3; %this defines a function f of a single variable x %What is the exact value of the integral of f from 0 to 1.5? %Compute it by hand, and store the result in a variable. exactValue = 1.5^4/4 %<--- your answer here figure('Name','Riemann sums'); %this line creates a new figure hold on;%tells Matlab to display several plots on the same figure %Plot f on the interval [0..1.5] t=[0:0.01:1.5]; plot(t,f(t)); %Compute the left Riemann sum for f on the interval [0..1.5] with N=5 %(i.e. by subdividing it into N = 5 intervals of equal length). N = 5; %Compute dx, the length of the sub-interval (aka steps size), in terms of N dx = (1.5 - 0)/N; %Set up an array with x values ranging from 0 to 1.5 with step size dx x=[0:dx:1.5]; %Store the first N values (all but last) in another array xLeft = x(1:end-1); %Compute the sum using the array with the first N values sumLeft = sum(f(xLeft).*dx) %Is this an overestimate or underestimate? Why? disp('This is an UNDERestimate because the function is increasing on 0..1.5'); %The following function will plot a staircase graph (don't worry about how it works): steps = @(x,y) plot(reshape([x(1:end-1);x(2:end)],1,[]),reshape([y;y;],1,[])); %Usage: steps(x,y) %x - an array of numbers %y - an array of numbers, having one less value than x %output: plots the step function whose value on [x(i)..x(i+1)] is y(i) % for i=1..length(x) %Example (run this script, then type in command line): %steps([1 2 3 4], [1 2 3]) %The left Riemann sum can be seen as the area under a staircase plot %Use the steps function above to plot this staricase. %Hint: use the array with all x values as the first argument, %and array with values of f on the left endpoints as the second argument. steps(x,f(xLeft)); %Compute the right Riemann sum for f on the inteval [0..1.5] with N = 5 xRight = x(2:end); sumRight = sum(f(xRight).*dx) %Plot the step-function whose area is given by this sum steps(x,f(xRight)); %Is this an overesimate or underesimate? Why? disp('This is an OVERestimate because the function is increasing on 0..1.5'); %Compute the averate of the above two sums. %This is called the "trapezoid approximation", since the mean of areas of %two rectangles with the same base is the area of the trapezoid. sumTrap = (sumRight + sumLeft)/2 %Is this an overestimate or underestimate? Why? disp('This is an OVERestimate because the function is CONCAVE UP on 0..1.5'); %This approximation is simply the area of the piecewise-linear %approximation obtained by connecting the dots (x0,f(x0)), (x1,f(x1)),.. %Plot this piecewise linear function. Hint: plot(x,y) %does what you want: connects (x(1), y(1)), (x(2),y(2)), (x(3),y(3)),... plot(x,f(x)); %What is the error, as a percentage of the true value? %That is, if ST is the trapezoid sum, and A is the value of the integral, %find |ST-A|/A error = abs((sumTrap - exactValue)/exactValue) %Experiment by changing the value of N above. Set N = 10,20,30 and re-run the script. %What happens to approximation as N increases? disp('Approximation becomes more precise as N increases.'); %Which value of N gives approximation that within 0.0001 of the true %value? disp('N=10000 is good enough for an answer within 0.0001 of the true value.'); %-----------PART 2: integrals from data-------------------------------------- figure('Name', 'Integrals from data'); %You are given the following numberic data (gx contains the values of g(x) for some function g) x=[-1.53791054834832,-1.49569810068615,-1.16989017405482,-1.14255885947370,-1.13895608794648,-1.12132996518602,-1.01239961679621,-0.845644131020566,-0.751398018530839,-0.511654284156889,-0.507415971326562,-0.344861415487210,-0.316428672889217,-0.185957360453133,-0.173007337607668,-0.0460550662940558,0.00635141688703844,0.0837915499445878,0.104852877827265,0.148214568125196,0.298266503318215,0.425661058965354,0.798414645773748,0.875818517048553,0.948581873231802,0.985349484833958,1.11465121173926,1.21024273817800,1.27955837883071,1.46202681067196]; gx=[0.0939334379248379,0.106766314619003,0.254452011841628,0.271053042801056,0.273290220347042,0.284397921108716,0.358813334945164,0.489136348869598,0.568588114970200,0.769672556024332,0.773004067874842,0.887870485852825,0.904722415960850,0.966010920559311,0.970511973624385,0.997881178746198,0.999959660317194,0.993003565963587,0.989066088543726,0.978271971435618,0.914879508569152,0.834279052620699,0.528630305626131,0.464377223760203,0.406647903377131,0.378736863244691,0.288676866957447,0.231150218028945,0.194510400404625,0.117946706646648]; %Plot gx vs x plot(x,gx); %the values of x are in range [-pi/2..pi/2], and y=g(x) for some %funciton g. Approximate integral of g from -pi/2 to pi/2 by computing %the left and right riemann sums and their average. %You already have f evaluated on the subdivision, the only thing %different from before is that the intervals in the subdivision have %varying lengths. The diff() function can be used to compute them. disp('-----------------Part 2-------------------------'); %Left Riemann sum: sumLeft = sum(gx(1:end-1).*diff(x)) %Right Riemann sum: sumRight = sum(gx(2:end).*diff(x)) %Average of these sums: sumT = (sumLeft + sumRight)/2 %Plot the step function %-----------PART 3: random sampling-------------------------------------- figure('Name','Random sampling') h = @(x) exp(-x.^2); %this is an example of a Gaussian function. This might %be familiar to you as the "Bell Curve" N = 10000; a = -30; b = 30; xn = sort(rand(N,1)*(b-a)) + a; %this generates an array of N random numbers in the interval [a..b] %sorted in increasing order %plot h on [a..b] t = [a:0.001:b]; plot(t,h(t)); %Compute the left Riemann sum, right Riemann sum and their average. %Since the differences between successive points are not the same, use %the diff() funciton to obtain a list of differences. disp('-----------------Part 3-------------------------'); %Left Riemann sum: sumLeft = sum(h(xn(1:end-1)).*diff(xn)) %Right Riemann sum: sumRight = sum(h(xn(2:end)).*diff(xn)) %Average of the two (a.k.a. trapezoidal approximation): sumT = (sumLeft + sumRight)/2 %Compute the square of this approximation: approxSqr = sumT.^2 %Increase N to 500, 1000, 10000. Does the square of the approximation seem %to approach anything? disp('The approximation approaches pi.'); %-------------------------PART 4: Exploring-------------------- figure('Name', 'Exploring 1/x'); f = @(x) 1./x; %we'll study the integral of this function by crunching numbers %plot f from 1 to 10 t = [1:0.001:10]; plot(t,f(t)); a = 1.5; b = 2.5; %approximate the integral of f by a left Riemann sum with dx=0.001 %on intervals [1..a], [1..b], [1..a*b] dx=0.001; %Array with x values from 1 to a with step dx: xa = [1:dx:a]; %Array with x values from 1 to ab with step dx xb = [1:dx:b]; %Array with x values from 1 to a*b with step dx xab = [1:dx:a*b]; %Area under the curve from 1 to a (approximate by a Riemann sum with step dx): Sa = sum(f(xa).*dx) %Area under the curve from 1 to b (approximate by a Riemann sum with step dx): Sb = sum(f(xb).*dx) %Area under the curve from 1 to a*b (approximate by a Riemann sum with step dx): Sab = sum(f(xab).*dx) %Try several more values of a and b (change them above), %and record results in the table below: disp(' Sa | Sb | Sab'); disp('-------|-------|--------'); disp('1.5047 | 1.2534|2.7574'); disp('0.6939 | 0.6939|1.3869'); disp('2.4854 | 1.6100|4.0949'); %What conclusion can you make about relationship between Sa, Sb and Sab ? disp('Sab = Sa * Sb'); %Let An be the area under the curve on the interval [1..2^n] %Compute An for n = 1 2 3 4 via a Riemann sum approximation with step dx x = [1:dx:2]; A1 = sum(f(x).*dx) x = [1:dx:4]; A2 = sum(f(x).*dx) x = [1:dx:8]; A3 = sum(f(x).*dx) x = [1:dx:16]; A4 = sum(f(x).*dx) %Plot n vs. An for n = 1, 2, 3, 4 n = [ 1 2 3 4]; An = [A1 A2 A3 A4]; figure('Name', 'Plot of A_n for n=1..4'); plot(n, An); %What conclusion can you make from this about the value of An? disp('Conclusion: A_n = n*A_1.'); %Recall that if 2^y = x, then y = log_2(x) %Therefore, integral_1^x f(t) dt = A_? (fill in the question mark) disp('=> integral_1^x f(t) dt = A_{log_2(x)}'); %Using this and your observation above, write a formula for % integral_1^x f(t) dt in terms of A_1. disp('So integral_1^x f(t) dt = log_2(x) * A_1.');
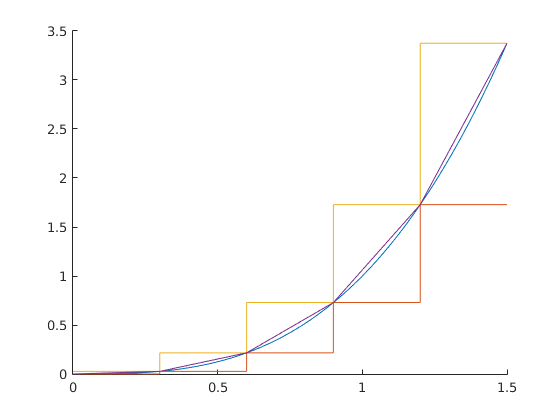
-----------------Part 1-------------------------
exactValue =
1.2656
sumLeft =
0.8100
This is an UNDERestimate because the function is increasing on 0..1.5
sumRight =
1.8225
This is an OVERestimate because the function is increasing on 0..1.5
sumTrap =
1.3162
This is an OVERestimate because the function is CONCAVE UP on 0..1.5
error =
0.0400
Approximation becomes more precise as N increases.
N=10000 is good enough for an answer within 0.0001 of the true value.
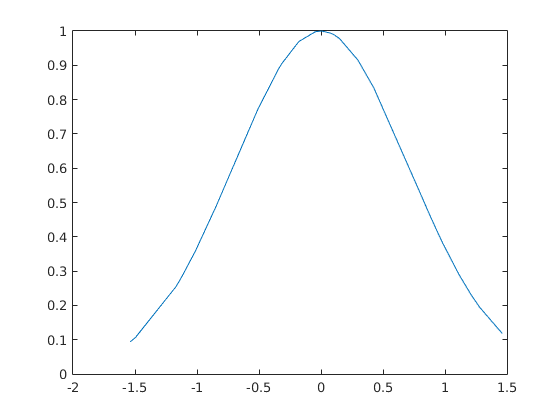
-----------------Part 2-------------------------
sumLeft =
1.7182
sumRight =
1.7052
sumT =
1.7117
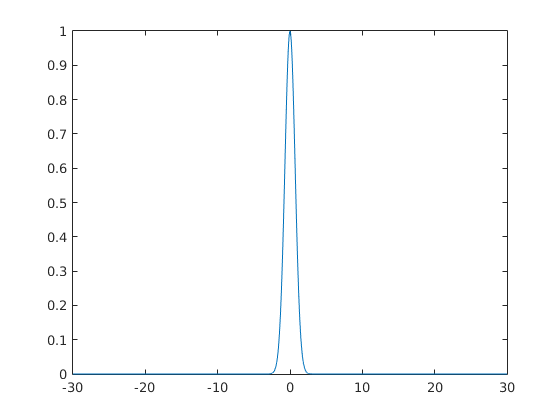
-----------------Part 3-------------------------
sumLeft =
1.7712
sumRight =
1.7737
sumT =
1.7724
approxSqr =
3.1416
The approximation approaches pi.
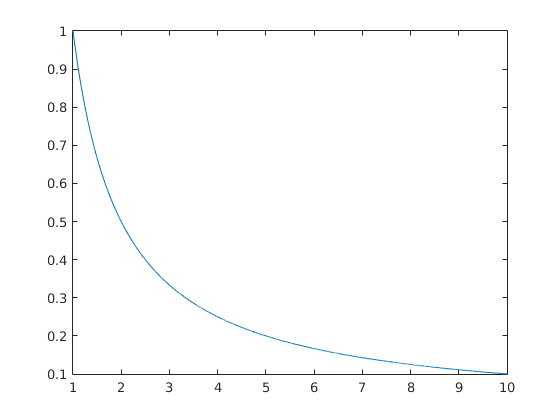
Sa =
0.4063
Sb =
0.9170
Sab =
1.3224
Sa | Sb | Sab
-------|-------|--------
1.5047 | 1.2534|2.7574
0.6939 | 0.6939|1.3869
2.4854 | 1.6100|4.0949
Sab = Sa * Sb
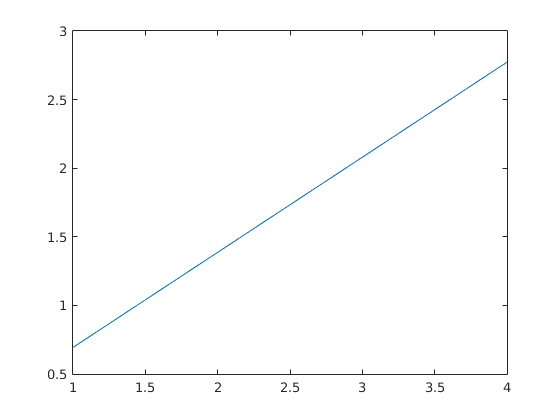
A1 =
0.6939
A2 =
1.3869
A3 =
2.0800
A4 =
2.7731
Conclusion: A_n = n*A_1.
=> integral_1^x f(t) dt = A_{log_2(x)}
So integral_1^x f(t) dt = log_2(x) * A_1.