%%MATLAB ASSIGNMENT 2: DERIVATIVES REVISITED %Welcome to MATLAB assignment 2, where calculus is made real %The "real" numbers as you know them are an illusion, or a very useful %convention. The physical universe doesn't allow for arbitrary small %values. So, for this assignment, we just agree that the smallest value %we'll deal with is... dx = 0.0001; %..and use it to define everything else. For example, the differential: d = @(f,x) f(x+dx) - f(x); %d(f,x) computes df(x). You have seen the notation "du" in your %substituiton rule, but it was very loosely defined. Here, df(x) is a very %concrete difference. %What is this difference good for? Well, the derivative is just the ratio %df/dx. See for yourself: f = @(x) x.^2; %we define a function f = x^2 should_be_six = d(f,3)/dx %this computes df/dx(3) -- what should the value be? %This lab will revisit the derivative and its connection to the integral.
should_be_six =
6.0001
%PART 1: THE FUNDAMENTAL THEOREM OF CALCULUS %------------------------------------------------------------------------- %Define a function int(f,a,b) that computes the integral numerically with %step size equal to dx %int(f,a,b) should return the integral of f from a to b %HINT: use your knowledge from previous lab. You don't need to bother with %left / right sums since the value of dx is small; an extra summand won't %affect the precision much. %You can put an anonymous function definition here, or make a function file. %If you choose to do it with an anonymous function, int = @(f,a,b) sum(f([a:dx:b])).*dx;
%Define a function f = x^3. Compute its integral from 0 to 1 using your %function. Verify that the value is what it should be. f = @(x) x.^3;
%Integral of f from 0 to 1 using your int(): int_f_0_1 = int(f,0,1) %True value (computed by hand): true_value = 1/4 %Here, I define a new function in terms of yours: df = @(x) d(f,x);
int_f_0_1 =
0.2501
true_value =
0.2500
%Compute the integral of df(x)/dx from 0 to 1, 2, 3 using your integral %function. Verify that the values are what they should be according to FTC. % HINT: define a new function g = df(x)/dx, and integrate it. %Alternatively, compute the integral of df, and divide by dx %(MATLAB is stupid, and df./dx is not a valid expression in MATLAB) g = @(x) df(x)./dx;
%Integral of df from 0 to 1:
int_df_1 = int(g,0,1)
int_df_1 =
1.0003
%Should be equal to this according to FTC:
v1 = f(1) - f(0)
v1 =
1
%Integral of df from 0 to 2:
int_df_2 = int(g,0,2)
int_df_2 =
8.0012
%Should be equal to this according to FTC:
v2 = f(2) - f(0)
v2 =
8
%Integral of df from 0 to 3:
int_df_3 = int(g,0,3)
int_df_3 = 27.0027
%Should be equal to this according to FTC:
v3 = f(3) - f(0)
v3 =
27
%Let's go the other way around! %Define F = integral from 0 to x of f using your int function %(F is a function of x) F = @(x) int(f,0,x);
%Now compute d/dx(F(x)) for x = 1, 2, 3 USING the d(f,x) function defined %above, Verify that the values are what they should be. % NOTE: use the d() function to compute this numerically
%d/dx(F(x)) at x = 1 is...
f1=d(F,1)./dx
f1 =
1.0003
%Should be equal to this according to FTC:
v1 = f(1)
v1 =
1
%d/dx(F(x)) at x = 2 is...
f2=d(F,2)./dx
f2 =
8.0012
%Should be equal to this according to FTC:
v1 = f(2)
v1 =
8
%d/dx(F(x)) at x = 3 is...
f3=d(F,3)./dx
f3 = 27.0027
%Should be equal to this according to FTC:
v1 = f(3)
v1 =
27
%PART 2: THE SUBSTITUTION RULE %------------------------------------------------------------------------- %define a function u = x^2 u=@(x)x.^2;
%Compute the integral of cos(u(x)) du from 0 to sqrt(pi/6) using your the %d() function defined above and your int() function % HINT: define a function g = cos(u(x)) du(x)/dx, (use the d() function!), % and plug it into your int(). % This will compute integral of cos(u(x)) du/dx dx = cos(u) du % NOTE: don't differentiate / integrate by hand. g = @(x) cos(u(x)).*d(u,x)./dx; int_f = int(g,0,sqrt(pi/6))
int_f =
0.5001
%Verify that the integral is what it should be according to the substitution rule. %What should the value of the integral be? (now, compute it by hand):
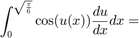
true_value = 0.5
true_value =
0.5000
%PART 3: WE DIDN'T LIE, DERIVATIVES REALLY GIVE YOU TANGENTS %------------------------------------------------------------------------- figure('Name', 'Tangent and normal'); %Define f = sqrt(x) and plot it between 0 and 4 f= @(x) sqrt(x); t=[0:0.001:4]; plot(t,f(t)); hold on; axis equal; %sets axis scaling to 1:1 (so the figure is not stretched)
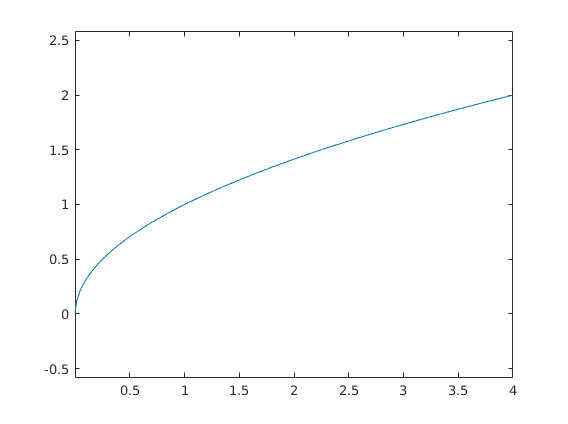
%Use the segment command to draw the TANGENT line to the plot at x = 1.5 % HINT: the slope is df/dx, so the direction vector is (dx, df) x = 1.5; segment(x,f(x),dx,d(f,x),3);
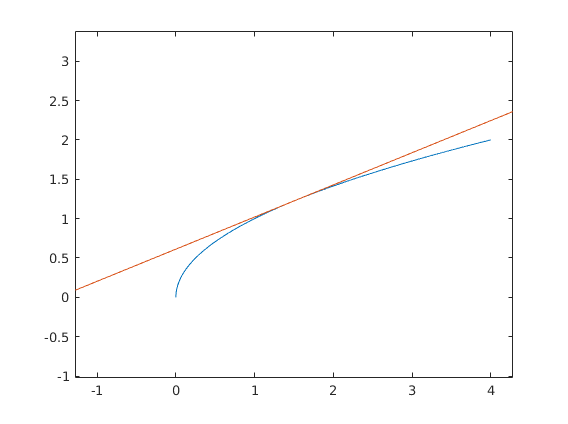
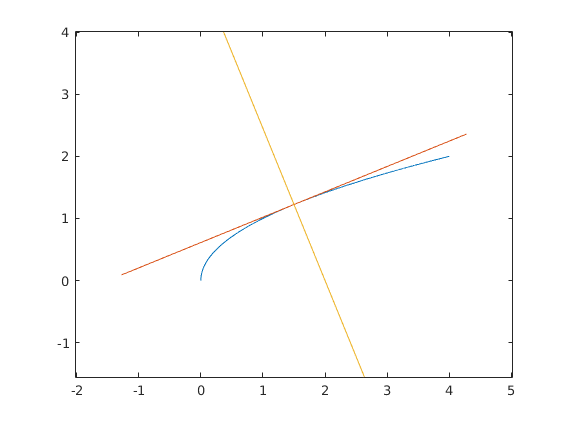
%Use the segment command to draw the NORMAL line to the plot at x = 1.5 % HINT: the slope is -dx/df segment(x,f(x),-d(f,x),dx,3);
%PART 4: ...AND TANGENTS GIVE YOU DERIVATIVES %------------------------------------------------------------------------- %Here we illustrate that the slope of the secant lines approaches the %derivative. % %Set f(x) = sin(x) and plot it between 0 and pi figure('Name', 'Derivative as limit of tangents'); f = @(x) sin(x); t = [0:0.001:pi]; plot(t,f(t)); hold on; axis equal;
%Now, we'll plot N secant lines with a FOR loop N = 20; %The secant lines go through (x0, f(x0)) and (x1, f(x1)) %x0 will be fixed: x0 = pi/3; %x1 will take different values between MAX=2 and x0 in the loop MAX = 2; for i = 0:N-1 %i runs from 0 to N-1 x1 = MAX - (MAX-x0)*i/N; %Compute the direction vector: %DX is the difference in X values: DX = x1 - x0; %DY is the difference in Y values: DY = f(x1) - f(x0); %Use the segment command to plot the tangent line: segment(x0,f(x0),DX,DY,2); end
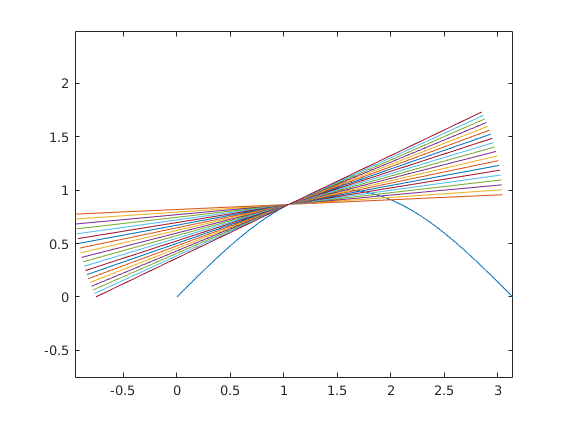
%Output DY/DX (this is last value it has taken in the loop) %and compare it to df/dx at x0 last_secant_slope = DY/DX tangent_slope = d(f,x0)./dx
last_secant_slope =
0.4792
tangent_slope =
0.5000
%PART 5: ENVELOPE %------------------------------------------------------------------------- figure('Name', 'Envelope'); %define f = x^2 and plot it between -1 and 1 f = @(x) x.^2; x=[-1:dx:1]; plot(x,f(x)) hold on ; axis equal;
%Draw tangents at 100 points between -1 and 1 % HINT: set up an array, and use a for loop to loop through it % NOTE: pick a nice value for L in the segment command - somethine % between 2 and 5, for example - whatever you think looks good for t=[-1:0.02:1] segment(t,f(t),dx,d(f,t),5); end %We say that the parabola is an envelope of its tangent lines.
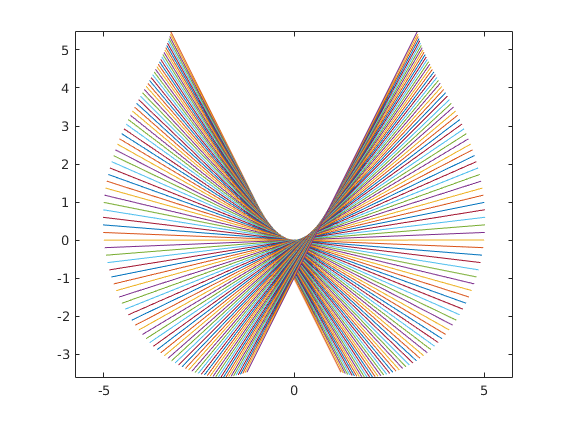
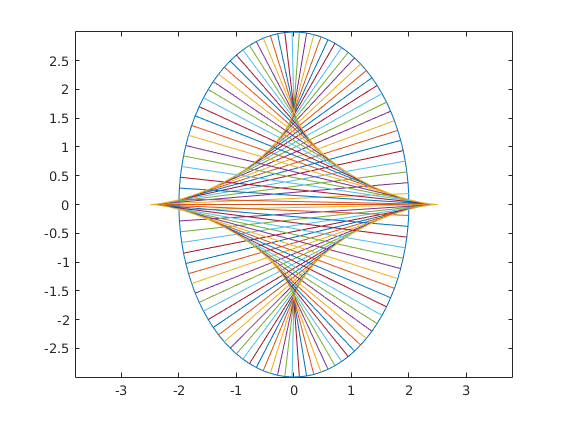
%PART 6: PARAMETRIC CURVE AS AN ENVELOPE OF ITS TANGENTS %------------------------------------------------------------------------- dt = dx; t = [0:dt:2*pi]; figure('Name', 'Parametric envelope'); %The following defines and plots an ellipse x1 = @(t) 3*cos(t); x2 = @(t) 2*sin(t); plot(x1(t),x2(t)); axis equal; hold on;
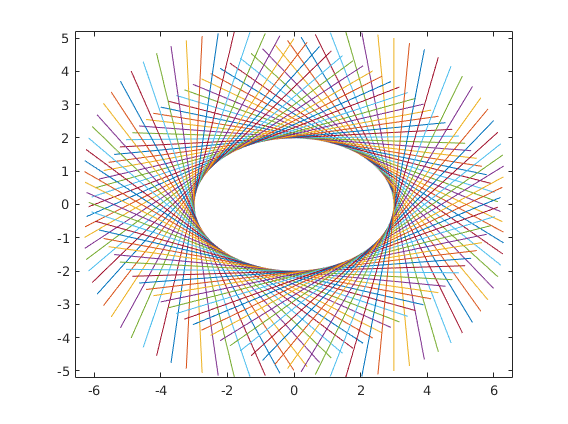
%Draw tangents at 100 equally spaced values of t between 0 and 2*pi % HINT: set up an array, and use a for loop to loop through it for t=linspace(0,2*pi,100) DX = d(x1,t); DY = d(x2,t); segment(x1(t),x2(t),DX, DY,5); end
%PART 6: PARAMETRIC CURVE NORMALS %------------------------------------------------------------------------- figure('Name', 'Normals to a curve'); %The following defines and plots an ellipse x1 = @(t) 2*cos(t); x2 = @(t) 3*sin(t); t=[0:0.01:2*pi]; plot(x1(t),x2(t)); axis equal; hold on;
%Draw normals at 100 equally spaced values of t between 0 and 2*pi % HINT: set up an array, and use a for loop to loop through it % NOTE: set the L argument of the segment command to be 5 or greater for % a nice picture for t=linspace(0,2*pi,100) DX = d(x1,t); DY = d(x2,t); segment(x1(t),x2(t),-DY, DX,5); end
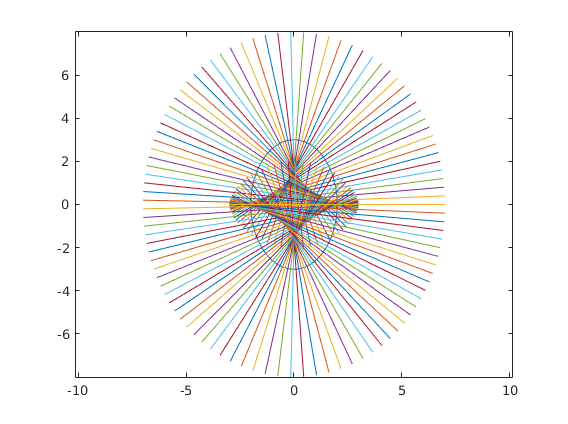
%Notice the shape that is formed inside. Is it smooth? Describe it here:
%Extra credit: define 5 closed parametric curves. Try making a conclusion %about the shape in the middle: what is a characteristic shared by all %of them? %%PART 7: EVOLUTES ------> EXTRA CREDIT, WORTH 1/2 LAB %This section is a study of the curve in the previous section. %If you think about it, what your eyes see is the curve formed by %intersection points of consecutive normals. That is, the evolute is the %<b>envelope</b> of the normals. Now, we just have to do the opposite of %what we did in parts 4 and 5: given a family of lines, we construct %a curve to which they are all tangent.
%The tedious part: given two lines: %L0 goes through (x0, y0) and has direction vector (a0, b0) %L1 goes through (x1, y1) and has direction vector (a1, b1) %What are the coordinates of the intersection point P? %P satisfies: P = [x0 y0] + t0[a0 b0] = [x1 y1] + t1[a1 b1] %for some constants t0, t1. Set up and solve the system of linear equations %for t0 and t1; obtain P as a function of all other variables P = @(x0,y0,a0,b0,x1,y1,a1,b1) [x0; y0] + [a0 0; b0 0]*([a0 -a1; b0 -b1]\[x1-x0; y1-y0]) ;
%Use the function P to define a function PN which, given functions %x(t) and y(t) and values t0, t1, computes the intersection of normals %at t = t0 and t = t1 PN = @(x,y,t0,t1) P(x(t0),y(t0),-d(y,t0),d(x,t0),x(t1),y(t1),-d(y,t1),d(x,t1));
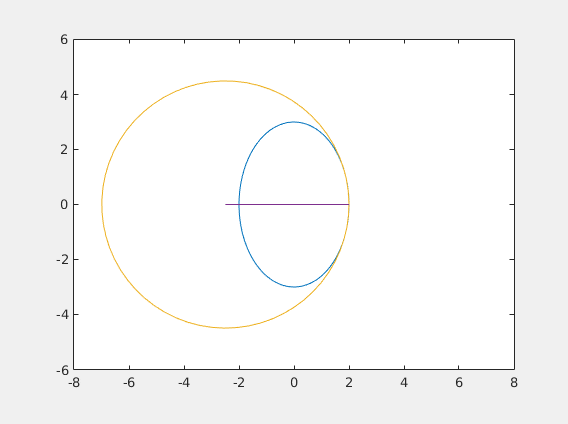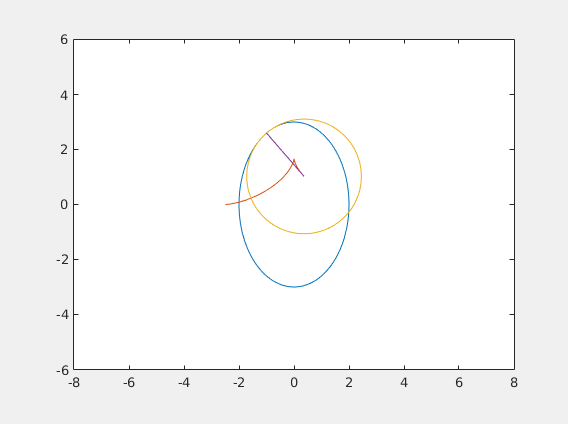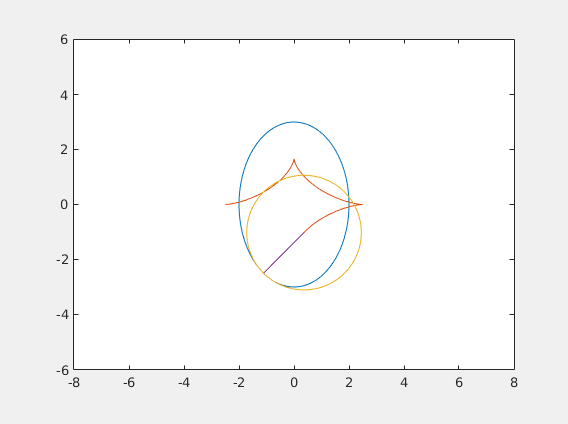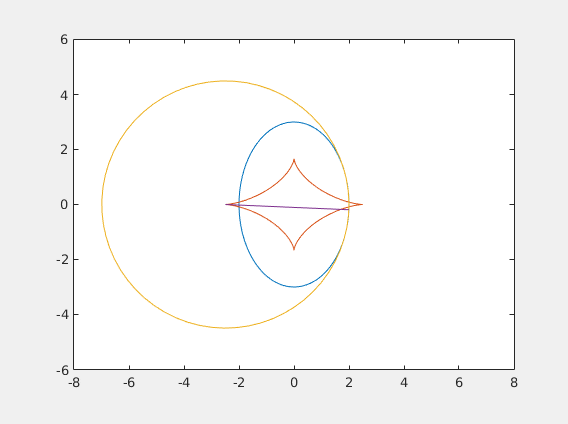
%Now we can use the function P to compute the points we want to plot. %(That's the fun part! :) ) %First, we define a curve: figure('Name', 'Evolute of an ellipse'); x = @(t) 2*cos(t); y = @(t) 3*sin(t); N=100; %Define an array t of size N with numbers going from 0 to 2*pi t = linspace(0,2*pi,N); %Plot (x(t), y(t)) plot(x(t),y(t)); axis equal; hold on; ex=zeros(N-1,1); %allocate an array for evolute x-points ey=zeros(N-1,1); %allocate an array for evolute x-points for i=1:N-1 %compute the intersection of normal through t(i) and t(i+1) intersection = PN(x,y,t(i),t(i+1)); %store the intersection point ex(i) = intersection(1); ey(i) = intersection(2); %connect the intersection point to the point on the curve at t(i) %HINT: plot([a c], [b d]) connects (a, b) to (c, d) plot([x(t(i)) ex(i)], [y(t(i)) ey(i)]); end %plot the evolute plot(ex, ey);
%Extra Extra credit (worth 1/4 of the lab), plus you get to make something %Wikipedia-article worthy % %Some math background first. % %The method of construction of the evolute above reveals its interesting %property: it is the locus of the centers of the osculating circles, %the circles that "kiss" the curve (from Latin "osculare" - to kiss). % %OK, hold on, let's talk about what this means first. % % %Just like there are tangent lines, there are tangent circles. %Unlike a tangent line, a circle tangent to a point is not unque - you can %draw many, by changing the radius (line can be thought of as a tangent %circle with infinite radius). % %If you draw a lot of circles and zoom at the common tangent point, you %will see that the larger circles are going on the _outside_ of the curve, %and the smaller circles are on the _inside_. %The one circle that is in between in the osculating circle. %It it the limit of the circles going through three points on the curve %as they approach each other. % %Note for physics people: a car going around the curve with unit speed will %experience the same acceleration at a point (x, y) as the car going around %the osculating circle at that point with the same speed. % %We say that the curve at that point and the circle have the same _curvature_. % %In other words, just as the line is the best linear approximation, the %circle is the best quadratic approximation. %--------------------------------------------------------------------------- %Write a circ(cx, cy, r) function that plots a circle of radius r centered at (cx, cy) %HINT: see how the ellipse is plotted. circ = @(cx, cy, r, w) plot(cx + cos([0:0.1:2.1*pi])*r, cy+sin([0:0.1:2.1*pi])*r); %Write a function dist(x0, y0, x1, y1) that computes the distance %from (x0, y0) to (x1, y1) dist = @(x0,y0,x1,y1) sqrt((x1-x0).^2 + (y1-y0).^2); %Time to get things moving! figure('Name', 'Evolute animated!'); for i = 1:N-1 %this sets up the animation loop. Each iteration will draw a new frame. %Plot the original curve (x(t), y(t)): plot(x(t),y(t)); axis equal; axis ([-8 8 -6 6]); hold on; %Plot a part of the evolute from time t=t(1) to t = t(i) %[NOTE: use the ex, ey arrays that are already computed plot(ex(1:i),ey(1:i)); %Compute the radius of curvature R at time t=i %(this is the distance from the point on the curve at time t=t(i) to the corresponding % point on the evolute): R = dist(ex(i),ey(i),x(t(i)),y(t(i))); %Draw a circle of radius R centered at the point on the evolute at time t(i): circ(ex(i),ey(i),R,1); %Plot a segment connecting the center of the circle to the correspoing %point on the curve (to which it will be tangent): plot([x(t(i)) ex(i)], [y(t(i)) ey(i)]); hold off; %allow the next frame to overwrite the figure pause(1/24); %pause before the next frame gets drawn %The code below saves the animation to an animated gif file. %Once you get the animation right, uncomment these lines %to get a nice .gif file that you can post on your Tumblr. %Submit the GIF file along with the assignment (ideally, edit the %published HTML file to include instead of the static figure). %------------------------------------------------------------------ %[A,map] = rgb2ind(frame2im(getframe(1)),256); %if i == 1; %imwrite(A,map,'evolute.gif','gif','LoopCount',Inf,'DelayTime',1/24); %else % imwrite(A,map,'evolute.gif','gif','WriteMode','append','DelayTime',1/24); %end end