Assignment3_solution

function [ ] = Assignment3()

%Assignment3 Matlab assignment 3
%%%%%%%%%%%%FUNCTIONS SECTION%%%%%%%%%%%%%%%%%%%%%
%%%%%DO NOT PUT CODE OUTSDIDE OF FUNCTIONS HERE%%%

%Write a function that finds zeros by bisection
%INPUT:   f : a continuous function of one variable
%       a,b : numbers such that the signs of f(a) and f(b) are opposite
%   epsilon : wanted precision (a small number)
%OUTPUT:  x : a number such that |f(x)|<epsilon
%    nsteps : number of steps it took to reach x
    function [x, nsteps] = find_zero_bisection(f, a, b, epsilon)
        if (sign(f(a)) ~= sign(f(b)))
           mid = (a+b)/2;
           val = f(mid);
           nsteps = 0;
           while (abs(val) > epsilon)
               if (sign(f(a)) == sign(val))
                   a = mid;
               else
                   b = mid;
               end
               mid = (a + b)/2;
               val = f(mid);
               nsteps = nsteps + 1;
           end
           x = mid;
       end
    end

root =

    2.8284


nsteps =

    17

%Finding zeros by Newton's method
%INPUT:   f : a differentiable function of one variable
%        x0 : an initial guess for the root
%   epsilon : wanted precision (a small number)
%OUTPUT:  x : a number such that |f(x)|<epsilon
%    nsteps : number of steps it took to reach x
    function [x, nsteps] = find_zero_Newton(f, x0, epsilon)
        h = 0.0001;
        df = @(x) (f(x + h) - f(x))/h;
        x = x0;
        nsteps = 0;
        while (abs(f(x)) > epsilon)
            x = x- f(x)/df(x);
            nsteps = nsteps + 1;
        end
    end

root =

    2.8284


nsteps =

     3

%Write a function that draws the involute of a curve (fx(t), fy(t)) starting form
%t=t0 to t=t1
    function draw_involute(fx, fy, t0, t1)
         t_step = 0.01;
         t = [t0: t_step : t1];
         N = length(t);
         L = 0; %this variable will store length of the curve so far
         iv_x = zeros(N,1); %N-by-1 array
         iv_y = zeros(N,1); %N-by-1 array
        for i = 2:N
            %compute dx, dy
            dx = fx(t(i)) - fx(t(i-1));
            dy = fy(t(i)) - fy(t(i-1));
            %first, update length
            dL = sqrt(dx^2 + dy^2);
            L = L + dL;
            %we have all the data now
            %the direction vector is (-dx, -dy), its length is dL, the
            %distance we need to go is L, and the starting point
            %is (x(t), y(t))
            iv_x(i) = fx(t(i)) - dx*L/dL;
            iv_y(i) = fy(t(i)) - dy*L/dL;
            %Optional: connect the point on the graph to the point on evolute
            plot([fx(t(i)) iv_x(i)], [fy(t(i)) iv_y(i)]);
        end
        plot(iv_x, iv_y);
    end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%Testing the bisection: test 1
    f  =  @(x) x.^2 - 8;
    [root, nsteps] = find_zero_bisection(f, 0, 5, 0.0001)

%Testing the bisection: test 2
    f  = @(x) 6 - x.^2;
    [root, nsteps] = find_zero_bisection(f, 0, 5, 0.0001)

root =

    2.4495


nsteps =

    14

%Testing Newton's
    f  =  @(x) x.^2 - 8;
    [root, nsteps] = find_zero_Newton(f, 2.5, 0.0001)

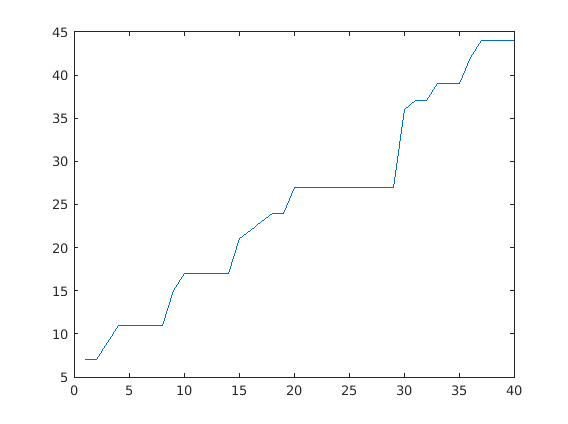
Let a_n = 0.1/2^n, and b_n = nsteps from calling
find_zero_bisection(f,0,5,a_n) for f  =  @(x) x.^2 - 8;
Plot n vs b_n for n = 1..40

figure('Name', 'Bisection vs. Newton step count');
f  =  @(x) x.^2 - 8;
for n=1:40
    an = 0.1/2^n;
    [root, nsteps] = find_zero_bisection(f,0,5,an);
    bn(n) = nsteps;
end
plot([1:40],bn);
hold on;

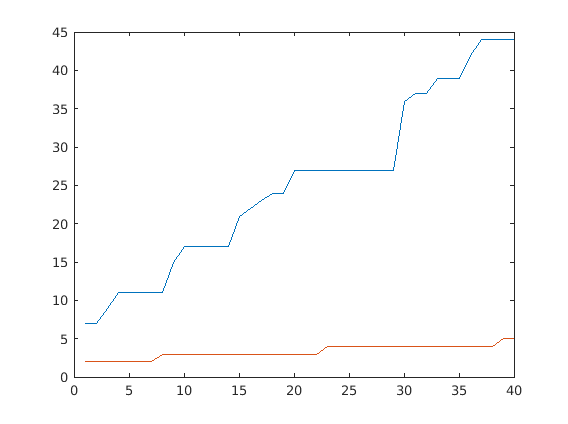
Let a_n = 0.1/2^n, and b_n = nsteps from calling
find_zero_Newton(f,2.5,a_n) for f  =  @(x) x.^2 - 8;
Plot n vs b_n for n = 1..40

for n=1:40
    an = 0.1/2^n;
    [root, nsteps] = find_zero_Newton(f,2.5,an);
    bn(n) = nsteps;
end
plot([1:40],bn);

%Testing the involute
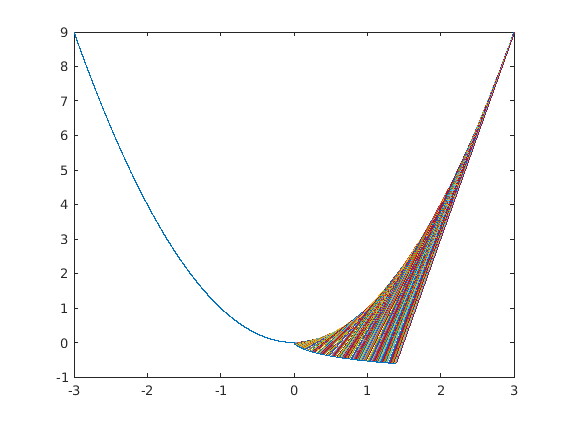
figure('Name', 'Involute of a parabola');
fx = @(t) t;
fy = @(t) t.^2;
%Plot the parabola:
t = [-3:0.001:3];
plot(fx(t), fy(t));
hold on;
draw_involute(fx,fy,0,3);

%Extra Credit (Worth 1/4 of lab)
% Let a_n = the volume of n-dimensional sphere. Compute a_n for n = 1..10
a = zeros(10,1);
a(1) = 2;
dH = 0.0001;
H = [-1:dH:1];
r = @(h)  sqrt(1-h.^2);
for dim = 2:10
   a(dim) = sum(a(dim-1).* r(H).^(dim-1) ).*dH;
end
a

end