Contents

Assignment 4 - DRIVER SECTION

This is the part of the code from which the tests are called

% UNCOMMENT THE CALLS TO TEST FUNCTIONS AS YOU COMPLETE THEM
function Assignment4()

        matlab_bug_workaround()

Series sum test

        partial_sum_test_1()
        partial_sum_test_2()

Sum of 1./2.^n from n = 0 to n = 20 is approximately 2:
S = 1.999999 
Exploring sum of inverses of squares
sqrt(6S) = 3.141583 

Sequences of iterates: a graphic approach

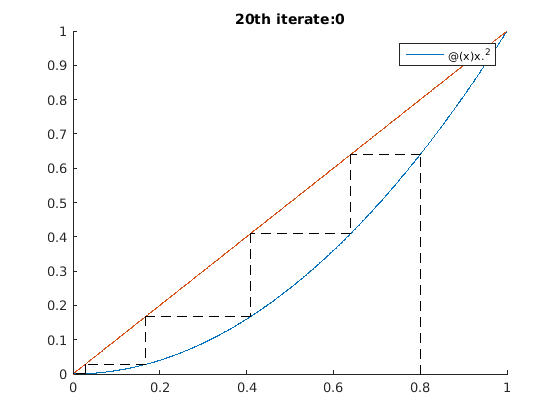
        iterates_test_1()
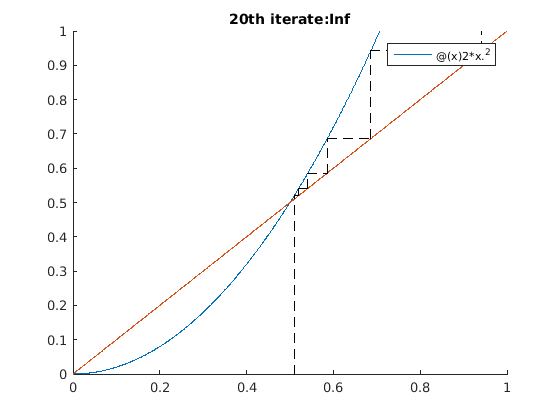
        iterates_test_2()
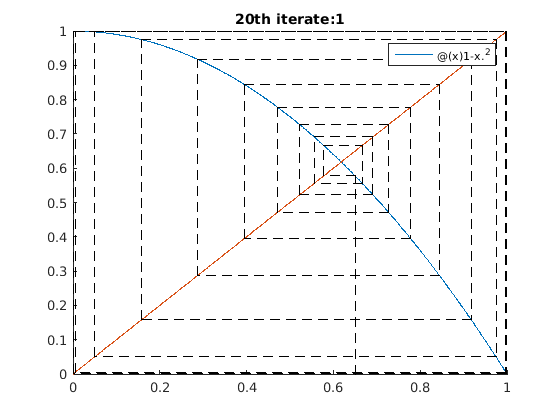
        iterates_test_3()
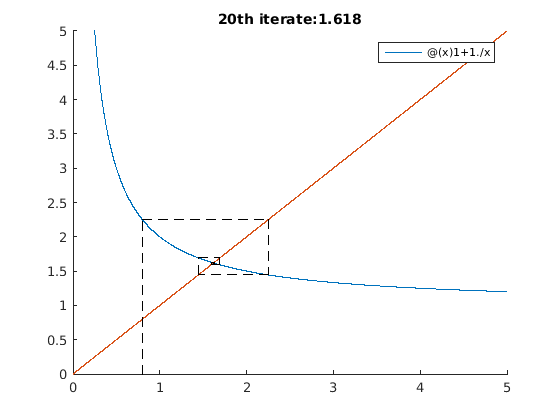
        iterates_test_4()
        iterates_test_5()
        iterates_test_6()

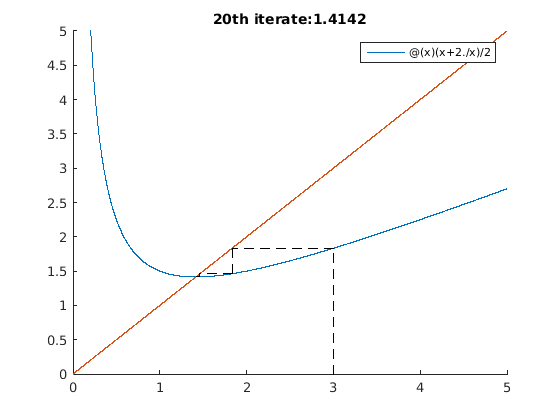
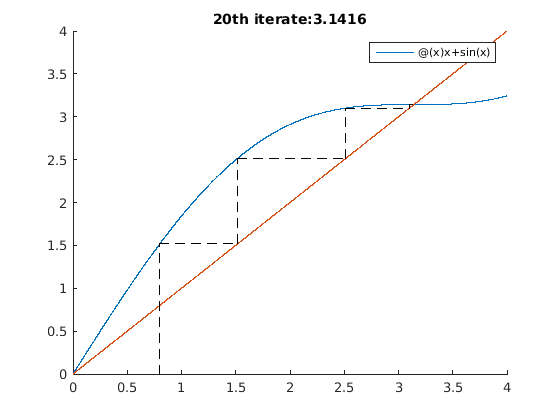
Extra credit

        extra_credit_test()

ans =

  -0.8090 + 0.5878i
   0.3090 - 0.9511i
   0.3090 + 0.9511i
   1.0000 + 0.0000i
  -0.8090 - 0.5878i

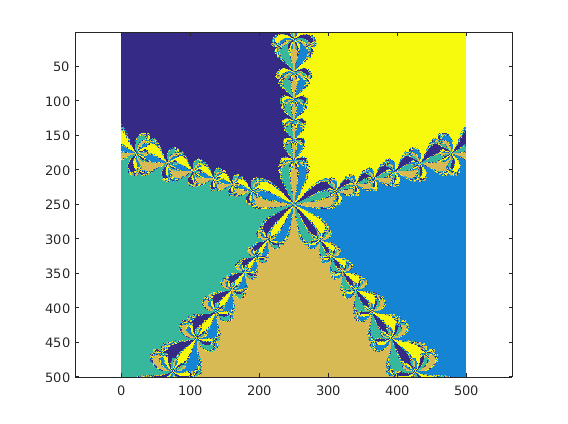
end

Functions section

This sections contains all the functions that you need to write

%%%DO NOT PUT CODE OUTSDIDE OF FUNCTIONS%%%%%%%%
%%%%%COMPLETE THE FUNCTIONS BELOW%%%%%%%%%%%%%%%
function [v]=dummy(a)
%dummy function helps to work around a bug in MATLAB publishing code
v = 2 + 2;
end


function [Pn] = partial_sum(f, k0, N)
    Pn = sum(f(k0:k0+N));
end



function seg(x0, y0, x1, y1)
    plot([x0 x1], [y0 y1], '--k');
end

function [x] = plot_iterates(f, x0, N)
    y = 0;
    x = x0;
    for i = 1:N
        seg(x, y, x, f(x));
        seg(x, f(x), f(x), f(x));
        y = f(x);
        x = y;
    end
end

function plot_func_and_iterates(f, window, x0, N)
    figure();
    hold on;
    a = window(1);
    b = window(2);
    x = [a:0.001:b];
    plot(x, f(x), x, x);
    legend(func2str(f));
    axis(window);
    L = plot_iterates(f, x0, N);
    title(strcat(num2str(N),'th iterate: ', num2str(L)));
end


function [pos] = search_approx(L, a, eps)
    pos = 0;
    for k=1:length(L)
       if(abs(L(k)-a) < eps)
           pos = k;
       end
    end
end

function root = newton(f, x0, nsteps)
    x  = x0;
    h  = 0.000001;
    for i = 1:nsteps
        x = x - f(x) / ( (f(x+h) - f(x))/h);
    end
    root = x;
end

function [roots] = draw_newton_fractal(f, bounds, N)
   roots = [];
   M = zeros(N);
   rval = linspace(bounds(1), bounds(2), N);
   ival = linspace(bounds(3), bounds(4), N);

    for r = 1:N
       for c = 1:N
           z = rval(r) + i*ival(c);
           root = newton(f, z, 200);
           pos = search_approx(roots, root, 0.2);
           if (pos > 0)
               M(r,c) = pos;
           else
               roots(end+1) = root;
               M(r,c) = length(root);
           end
       end
    end
    imagesc(M);
    axis equal;
    roots'
end

Tests section

This sections contains code that calls your functions to verify that they work as intended

function matlab_bug_workaround()
    %This is a workaround to bug #496201.
    dummy(1);
end


    function partial_sum_test_1()
        disp('Sum of 1./2.^n from n = 0 to n = 20 is approximately 2:');
        S = partial_sum(@(n) 1./(2.^n), 0, 20);
        fprintf('S = %f \n',S);
    end

    function partial_sum_test_2()
        disp('Exploring sum of inverses of squares');
        S = partial_sum(@(n) 1./(n.^2), 1,  100000);
        v = sqrt(6*S);
        fprintf('sqrt(6S) = %f \n',v);
    end


    function iterates_test_1()
        %The sequence of iterates approaches 0
        plot_func_and_iterates( @(x) x.^2, [0 1 0 1], 0.8, 20);
    end

    function iterates_test_2()
        plot_func_and_iterates( @(x) 2*x.^2, [0 1 0 1], 0.51, 20);
    end

    function iterates_test_3()
        plot_func_and_iterates( @(x) 1- x.^2, [0 1 0 1], 0.65, 20);
    end

    function iterates_test_4()
        plot_func_and_iterates( @(x) 1 + 1./x, [0 5 0 5], 0.8, 20);
    end
     function iterates_test_5()
        plot_func_and_iterates( @(x) (x + 2./x)/2,  [0 5 0 5], 3, 20);
     end

     function iterates_test_6()
        plot_func_and_iterates( @(x) x + sin(x),  [0 4 0 4], 0.8, 20);
    end


     function iterates_test_7()
        plot_func_and_iterates( @(x) 1 + 1./(1+x),  [0 4 0 4], 0.8, 20);
    end



function extra_credit_test()
    figure('Name','Newton Fractal for x^5-1');
    f = @(x) x^5 - 1;
    draw_newton_fractal(f, [-3, 3, -3, 3], 500);
end

Published with MATLAB® R2015a